הצפנת אל-גמאל
הסיכום על אל-גמאל נכתב כהכנה עצמית לבחינת הגמר בקורס ״מבוא לקריפטוגרפיה״, בדומה לסיכום הקודם בנוש ההצפנת RSA. הוא מתמקד (למרבה הפלא) בהצפנת אל-גמאל, שהיא מערכת הצפנה אסימטרית, ובחתימה דיגיטלית של אל-גמאל. הוא עוסק באבטחה סמנטית ובסיכונים של שימוש באל-גמאל, ומיועד בעיקר למי שכבר יש ידע בסיסי בנושא. אם אתם מוצאים שגיאות או רוצים להוסיף משהו, מוזמנים להשאיר לי פנייה באתר.
אבטחה סמנטית
אבטחה סמנטית היא תכונה מהותית במערכות הצפנה מודרניות. בבסיסה, היא עונה על השאלה: “האם תוקף יכול ללמוד משהו על ההודעה המקורית רק מההצפנה שלה?” אנחנו מצפים מהצפנה שלא תספק שום מידע נוסף על ההודעה המקורית מעבר למה שניתן ללמוד מההודעה עצמה. כמו שמבלוק אחד אנחנו נצפה שלא יהיה ניתן ללמוד כלום, כך גם מהרבה בלוקים נצפה שלא יהיה ניתן להפיק מידע נוסף.
מבחינה פורמאלית, המבחן המתמטי לאבטחה סמנטית (המכונה גם “אי יכולת להבחין” - Indistinguishability) מתואר כך:
- יש לתוקף שתי הודעות אפשריות $x_0$ ו-$x_1$
- אנחנו בוחרים באקראי $b \in {0, 1}$ ומצפינים את $x_b$
- התוקף מקבל את ההצפנה $E(x_b)$
- אם התוקף לא יכול לנחש איזו הודעה הוצפנה בסיכוי גבוה מ-50%, המערכת היא סמנטית בטוחה
ב-RSA קלאסי, הצפנה של אותה הודעה תמיד תייצר את אותו ערך מוצפן. זה אומר שאם התוקף רואה שתי הצפנות זהות, הוא יודע בוודאות שהן מגיעות מאותה הודעה מקורית - זו הפרה של אבטחה סמנטית. לדוגמה:
- אם אני מצפין את המספר 7 ב-RSA, אקבל תמיד אותה תוצאה (נניח 42)
- אם מישהו רואה שתי הצפנות שהן 42, הוא יודע שמדובר באותה הודעה
- גרוע מכך, אם התוקף יכול להצפין הודעות בעצמו (כי RSA הוא אסימטרי עם מפתח הצפנה פומבי), הוא יכול לבצע “מתקפת מילון” - להצפין את כל ההודעות האפשריות ולהשוות לטקסט המוצפן שברשותו
הצפנת אל-גמאל היא מערכת הצפנה אסימטרית שפותחה ב-1985 על ידי טאהר אל-גמאל והיא מבוססת על בעיית הלוגריתם הדיסקרטי. להצפנת אל-גמאל יש חשיבות רבה, בין היתר בגלל שלעומת RSA, היא מספקת אבטחה סמנטית. בכך, אל-גמאל מציע משהו שאין ב-RSA: אקראיות פנימית בתהליך ההצפנה.
כל הצפנה של אותה הודעה תיצור תוצאה שונה לחלוטין - וזו הסיבה שאל-גמאל מספק אבטחה סמנטית.
החשיבות של הצפנה מהסוג הזה נובעת מכך שבסכמות פומביות, כשלכולם יש את מפתח ההצפנה, אפשר לבדוק תכונות מעניינות באופן יחסית פשוט. מכאן שיש חשיבות למערכת שבה כל פעם שאני מציג את המידע המוצפן, הוא יהיה שונה.
הסיבה שהדבר הזה בכלל אפשרי, או באופן כללי - שניתן לקחת הצפנה ולשנות אותה, נובעת מכך שהאיבר האקראי גורם ליותר אפשרויות לייצוג של אותה הודעה מקורית.
עבור קלט מסוים, יש באופן עקרוני $p$ הצפנות אפשריות, כאשר $p$ הוא מספר האיברים. מדובר במספר עצום של הצפנות, אבל כולן מתפענחות חזרה לאותו ערך. זה קורה כי כל הצפנה מורכבת בעצם משני ערכים, אך התחום שלה גדול יותר. יש יותר אפשרויות במה שאתה מצפין. בגלל האיבר האקראי, אורך הפלט תמיד גדול יותר, ולכן יש יותר אפשרויות לייצוג של אותה הודעה מקורית.
זה דומה לביצוע פעולת “דאבל DES” אבל עם אותו מפתח - כלומר, להפעיל את אלגוריתם ה-DES פעמיים עם אותו מפתח. יש לנו $p$ אפשרויות להצפנה, כי האיבר האקראי $R$ יכול לקבל כל אחד מהערכים בחבורה, וכולם מתפענחים חזרה לאותה הודעה מקורית.
איך פועלת הצפנת אל-גמאל?
| תרשים זרימה של אל-גמאל |
יצירת מפתחות
| תהליך יצירת מפתחות של אל-גמאל |
- בוחרים מספר ראשוני גדול $p$ (בד”כ מהצורה $p = 2q + 1$ כאשר $q$ גם ראשוני)
- בוחרים יוצר $\alpha$ בחבורה $\mathbb{Z}_p^*$, שגודלה אגב הוא $p-1$. יש טכניקות למציאת יוצר כזה.
- בוחרים מספר אקראי $a$ - המפתח הפרטי. הוא יהיה בחזקה של היוצר, והטווח שלו הוא $0 \leq a \leq p-2$
- נגדיר $\beta = \alpha^a \bmod p$. המפתח הפומבי: $(p, \alpha, \beta)$
המפתח הפרטי:
\[a\]המפתח הפומבי:
\[(p, \alpha, \beta)\]
הצפנה
| דוגמה להצפנת אל-גמאל |
נניח שבוב רוצה לשלוח הודעה $x\in \mathbb{Z}_p^*$ לאליס. נניח שאליס שמחזיקה במפתח הפרטי $a$. ושלבוב יש את המפתח הפומבי שלה - $(p, \alpha, \beta)$.
- הוא בוחר מספר אקראי $k$ (וזאת הסיבה לאבטחה הסמנטית!), בטווח $0 < k < p-1$
- מחשב $y_1 \equiv \alpha^k \pmod{p}$
- מחשב $y_2 \equiv x \cdot \beta^k \pmod{p}$
- ההצפנה הסופית היא הזוג $(y_1, y_2)$
כל הצפנה של אותה הודעה תייצר זוג $(y_1, y_2)$ שונה לחלוטין, בזכות בחירת $k$ אקראי בכל פעם.
פענוח
 |
|---|
| דוגמה לפיענוח אל-גמאל |
אליס, בעלת המפתח הפרטי $a$, מקבלת את ההצפנה $(y_1, y_2)$ ומחשבת:
\[x \equiv y_2 \cdot (y_1^a)^{-1} \pmod{p}\]להבנה אינטואיטיבית של תהליך הפענוח:
- $y_2 = x \cdot \beta^k = x \cdot (\alpha^a)^k = x \cdot (\alpha^k)^a$
- $y_1^a = (\alpha^k)^a = \alpha^{ak} \rightarrow \left(y_1^a\right)^{-1} = \alpha^{-ak}$
- $y_2 \cdot (y_1^a)^{-1} = x \cdot (\alpha^k)^a \cdot \alpha^{-ak} = x \cdot 1 = x$
או כפי שהמרצה הדגיש: “אנחנו ‘מבטלים’ את האקראיות שהוכנסה בשלב ההצפנה.”
אפשר גם להסתכל על זה כך: ההודעה $x$ ממוסכת על ידי הכופל $\beta^k$, כלומר ש $y_2$ מעביר את ההודעה עם מיסוך. הפיענוח מסיר את המסכה באמצעות חלוקה של $y_2$ בחזקה המתאימה של $y_1$, שהיא בעצם המפתח הפרטי $a$ של אליס.
חתימה דיגיטלית של אל-גמאל
חתימה דיגיטלית של אל-גמאל שונה מההצפנה של אל-גמאל, אך עדיין מבוססת על אותם עקרונות.
יצירת מפתחות לחתימה
בדומה לצופן אל-גמאל:
- $p$ מספר ראשוני שעבורו בעיית DLp בחבורה $\mathbb{Z}_p^*$ קשה
- $\alpha$ הוא יוצר של $\mathbb{Z}_p^*$
- $a$ הוא המפתח הפרטי של אליס (מספר אקראי בטווח $0 \leq a \leq p-2$)
- נגדיר $\beta = \alpha^a \bmod p$. המפתח הפומבי הוא $(p, \alpha, \beta)$
חתימה
כדי לחתום על הודעה $x$:
- אליס בוחרת מספר אקראי $k$ שהוא זר ל-$(p-1)$ (כלומר $\gcd(k, p-1) = 1$). אם הוא זר, היא מחשבת את ההופכי שלו $k^{-1} \bmod (p-1)$
-
אליס חותמת על ההודעה $x$ ועל הערך האקראי שהגרילה. החתימה כוללת:
\[\begin{aligned} \gamma &= \alpha^k \bmod p \\ \delta &= (x - a\gamma) \cdot k^{-1} \bmod (p-1) \end{aligned}\] - אליס שולחת לבוב את ההודעה ביחד עם החתימה (בלי $k$) - $\left(x,\left(\gamma, \delta\right)\right)$
אימות חתימה
לאחר שבוב מקבל את $x$, שלמעשה הוא ערך התמצות של ההודעה (פלט של פונקציית צמצות), הוא בודק שאכן:
\[\beta^{\gamma} \cdot \gamma^{\delta} \equiv \alpha^x \pmod{p}\]הכוחה לנכונות ניתן למצוא בויקיפדיה.
סיכונים בשימוש באל-גמאל
מציאת המפתח הפרטי במקרה ש$k$ נחשף
חשיפת $k$ מאפשרת לחלץ את המפתח הפרטי $a$ באופן הבא:
מ-$\delta$ אנחנו יודעים:
\[\delta = (x - a\gamma) \cdot k^{-1} \pmod{p-1}\]נכפיל ב-$k$ משני הצדדים ונקבל:
\[\delta \cdot k = (x - a\gamma) \pmod{p-1}\]נפתור עבור $a$:
\[a = \frac{\delta \cdot k - x}{-\gamma} \bmod (p-1)\]שימוש חוזר באותו $k$
ניתן לחלץ את המפתח הפרטי גם במקרה שידוע ששתי הודעות שונות נחתמו עם אותו $k$ ואפילו אם הודעה אחת נחתמה עם $k$ והשנייה עם $k+2$.
נסתכל על מה שקורה - יש לנו שני חלקים בהצפנה:
\[\begin{aligned} c_1 &= \alpha^k \\ c_2 &= x \cdot \beta^k \end{aligned}\]- $\alpha$ זה מספר ציבורי
- $\beta = \alpha^a \mod p$
- $k$ זה ערך רנדומלי שאנחנו בוחרים כל פעם מחדש
- $x$ זו ההודעה
נניח שכל פעם יש הודעה חדשה, אבל הערך של לא משתנה $k$. אז אם:
- $\alpha^k$ קבוע
- ו־$x \cdot \beta^k$ משתנה עם ההודעה
תוקף שמאזין לקו יכול להשתמש במתקפת Chosen plaintext / Ciphertext. נניח שהיריב משתמש במתקפה כמו chosen plaintext: הוא בוחר הודעה $x$, ומבקש את ההצפנה שלה. הוא מקבל:
אם $x$ ידוע — אפשר לחשב את ההופכי של $x$, כי אנחנו עובדים בתוך החבורה $\mathbb{Z}_p^*$, ולכל איבר יש הופכי. לכן:
\[\beta^k = \frac{c_2}{x} \mod p\]למה זה מסוכן?
\[\frac{c_2'}{\beta^k} = x'\]עכשיו כל פעם שיש הודעה חדשה עם אותו $k$, כלומר $c_2’ = x’ \cdot \beta^k$, אפשר לבטל את $\beta^k$ (שכבר חושב), ולקבל את ההודעה עצמה:
זאת הבעיה המרכזית: כל הודעה עם אותו $k$ — ניתנת לפענוח מיידי.
שימוש חוזר בערך קרוב ל-$k$
נניח ש־$k_{\text{חדש}} = k + 2$ האם זה פותר את הבעיה?
לא באמת. כי אז: \(\beta^{k+2} = \beta^k \cdot \beta^2\)
ואם התוקף כבר יודע את $\beta^k$, והוא יודע את $\beta$ (כי זה ציבורי), אז הוא גם יודע את $\beta^2$, ויכול לחשב את כל הביטוי. כלומר גם קשר בין ערכי $k$ זה מסוכן.
ומה עם מספר ערכי $k$ אפשריים?
אנחנו עובדים ב־$\mathbb{Z}_{p-1}$, אז ל־$k$ יש: \(p - 2\) ערכים שונים לכל היותר.
אם $p$ בגודל של 1024 ביט ומעלה — זה המון. אבל זה עדיין מרחב סופי. אי אפשר להצפין אינסוף הודעות עם ElGamal בלי לחזור על ערכי $k$.
מסקנה
אם פעם אחת השתמשתי ב־$k$ מסוים והיריב למד ממנו — כל הודעה שאצפין שוב עם אותו $k$ — חשופה. גם אם יש לי המון הודעות, וגם אם היריב זוכר רק חלק מהן — יש סיכון ברגע ש־$k$ חוזר.
שינוי בצופן ElGamal: חיבור במקום כפל (יכול להיות בטוח)
במקום להצפין את החלק השני של ElGamal (ה־$Y$) עם כפל, נצפין אותו עם חיבור. כלומר, במקום:
\[c_2 = x \cdot \beta^k\]נשתמש ב־:
\[c_2 = x + \beta^k\]
האם הצופן הזה בטוח?
בכל פעם נבחר ערך $k$ חדש ורנדומלי. השאלה היא: האם ההצפנה הזאת בטוחה כמו ElGamal המקורי?
שני מצבים לבחינה
- צד המפענח (בעל המפתח הפרטי $a$)
-
המפענח יודע את $a$, ולכן יכול לחשב:
\[\beta^k = (\alpha^a)^k = \alpha^{ak}\] -
ואז הוא עושה:
\[x = c_2 - \beta^k\]
כלומר, הפענוח עובד תקין. במקום כפל בהופכי (כמו בצופן המקורי), עושים פשוט חיסור.
-
-
צד התוקף
אם התוקף רואה את $\alpha^k$ ואת:
\[c_2 = x + \beta^k\]- הדרך היחידה שלו ללמוד משהו על $x$ היא לנחש את $\beta^k$.
-
אבל גם כאן, כמו ב־ElGamal המקורי, קיימת בעיית הלוגריתם הדיסקרטי: \(\beta = \alpha^a \Rightarrow \beta^k = \alpha^{ak}\)
- מבלי לדעת את $a$, לא ניתן לחשב את $\beta^k$.
כלומר: אין יתרון לתוקף בגלל השימוש בחיבור במקום כפל.
מתי זה לא בטוח?
אם במקום לבחור ערך $k$ חדש בכל פעם, נשתמש באותו $k$ שוב ושוב…
-
התוקף יכול לעשות כמו קודם: \(x' = c_2' - \beta^k\)
-
ואז עבור כל הודעה נוספת $c_2’’$, לחשב את $x’’$.
בדיוק כמו במצב הקודם — אם $k$ חוזר, יש דליפת מידע חמורה.
מה ההבדל האמיתי?
- ElGamal הרגיל מבוסס על כפל:
- הצפנה: $c_2 = x \cdot \beta^k$
- פענוח: $c_2 \cdot (\beta^k)^{-1}$
- הגרסה עם חיבור:
- הצפנה: $c_2 = x + \beta^k$
- פענוח: $c_2 - \beta^k$
שני המקרים נשענים על אותה בעיה קשה — למצוא $\beta^k$ מתוך $\alpha^k$, כלומר:
בעיית הלוגריתם הדיסקרטי (Discrete Log problem)
האם יש הבדל פרקטי?
- חיבור מהיר יותר מכפל? אולי.
- חיסור מהיר יותר מהכפלה בהופכי? כן.
- אבל:
- מה שגוזל את רוב הזמן זה לא הכפל/חיסור אלא חישוב הלוגריתם הדיסקרטי, שבלתי אפשרי במרחבים גדולים.
- לכן השוני כמעט לא משפיע על התוקף.
לסיכום:
| פעולה | ElGamal רגיל | גרסת החיבור |
|---|---|---|
| הצפנה | $x \cdot \beta^k$ | $x + \beta^k$ |
| פענוח | $c_2 \cdot (\beta^k)^{-1}$ | $c_2 - \beta^k$ |
| בטיחות | גבוהה (אם $k$ חדש) | גבוהה (אם $k$ חדש) |
| תלות ב־k | קריטית | קריטית |
- אם בוחרים כל פעם $k$ חדש — הצופן בטוח בדיוק כמו ElGamal.
- אם $k$ קבוע — קיימת אותה פגיעות בדיוק כמו בצופן המקורי.
הערה מהשיעור
“צופן ElGamal הוא למעשה צופן הזזה, רק במקום חיבור — אנחנו משתמשים בכפל. בגרסה הזו, החזרה לפעולת החיבור לא פוגעת בביטחון, כל עוד ממשיכים לבחור $k$ רנדומלי בכל פעם.”
סיכום
אל-גמאל מציע יתרונות משמעותיים לעומת RSA:
- אבטחה סמנטית - כל הצפנה של אותה הודעה נראית שונה לחלוטין
- מבוסס על בעיה קשה אחרת - לוג דיסקרטי במקום פירוק לגורמים ראשוניים, מה שמספק גיוון בהנחות הביטחון
- גמישות מתמטית - אפשר להשתמש בו לא רק בחבורות מודולריות, אלא גם בחבורות אחרות (כמו עקומים אליפטיים)
נקודות חשובות:
- אקראיות חיונית - האקראיות באל-גמאל (בחירת $r$ בהצפנה ו-$k$ בחתימה) היא קריטית לביטחון
- המחיר - ההצפנה כפולה בגודלה מההודעה המקורית (הצפנה היא זוג של ערכים)
- פעולות מודולריות - כל החישובים מתבצעים במודולו $p$ (להצפנה) או $p-1$ (לחתימה)
- הבנת היוצרים - חשוב להבין את תכונות היוצרים בחבורה מודולרית לצורך ביטחון המערכת
כפי שהמרצה סיכם לגבי הצפנת אל-גמאל: “שימו לב שאם אני אצפין את $M$ שוב ושוב, אני אקבל ערכים שונים לגמרי, כי כל פעם אני בוחר $r$ אחר. זה מה שנותן לנו את האבטחה הסמנטית.”
זה גם מסביר את המעבר שראינו בשנים האחרונות מ-RSA קלאסי למערכות חדשות יותר כמו RSA-OAEp (שמוסיף אקראיות ל-RSA) ואל-גמאל. אבטחה סמנטית הפכה לדרישה הכרחית במערכות הצפנה מודרניות.
המרצה הדגיש: “תראו מה זה, בעצם שיטת אל-גמאל, גם בחתימה, גם בהצפנה, נותנת לנו חוזק הרבה יותר ממה שהכרנו קודם. כל פעם החתימה נראית אחרת, אני מקבל גמא ודלתא אחרים לגמרי בתור חתימה. זה משהו מאוד חזק. בצד שני, אם איכשהו אני עולה על האקראיות או אם התוקף יכול להשפיע על האקראיות, אז הלכה…”
רקע טכני והרחבות מתמטיות
בעיית הלוגריתם הדיסקרטי: הבסיס התיאורטי
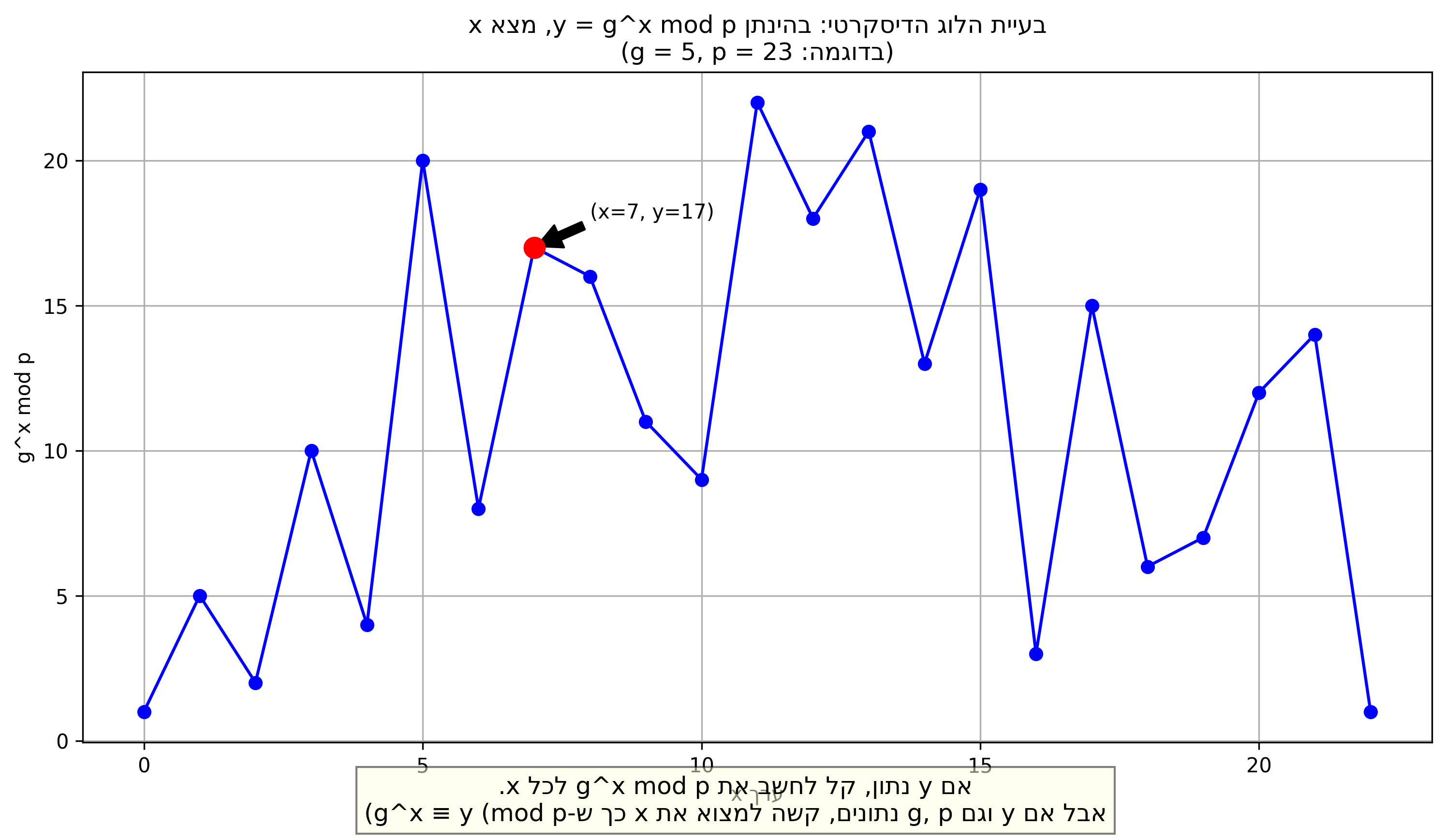
בעיית הלוגריתם הדיסקרטי היא הבסיס למערכות אל-גמאל: בהינתן $g$ (יוצר בחבורה מודולרית), $p$ (מספר ראשוני) ו-$y = g^x \bmod p$, משימה: מצא את $x$.
 |
|---|
| הבעיה של הלוגריתם הדיסקרטי |
מה זה יוצר בחבורה?
יוצר הוא איבר בחבורה שכאשר מעלים אותו בחזקות שונות, מקבלים את כל האיברים בחבורה. כפי שהמרצה הדגים עם $g=3$ במודולו 7:
- $3^0 \bmod 7 = 1$
- $3^1 \bmod 7 = 3$
- $3^2 \bmod 7 = 2$ (כי $9 \bmod 7 = 2$)
- $3^3 \bmod 7 = 6$ (כי $27 \bmod 7 = 6$)
- $3^4 \bmod 7 = 4$ (כי $81 \bmod 7 = 4$)
- $3^5 \bmod 7 = 5$ (כי $243 \bmod 7 = 5$)
- $3^6 \bmod 7 = 1$ (כי $729 \bmod 7 = 1$)
אנחנו רואים שהיוצר $g=3$ מכסה את כל האיברים השונים מאפס בקבוצה {1,2,3,4,5,6} לפני שהוא חוזר על עצמו. זוהי תכונה חשובה של יוצר.
לעומת זאת, לא כל איבר הוא יוצר. למשל, $g=2$ במודולו 7:
- $2^0 \bmod 7 = 1$
- $2^1 \bmod 7 = 2$
- $2^2 \bmod 7 = 4$
- $2^3 \bmod 7 = 1$ (כי $8 \bmod 7 = 1$)
רואים ש-$g=2$ מכסה רק את הערכים {1,2,4} - לא את כל הקבוצה! ולכן הוא אינו יוצר.
מספרים ראשוניים מיוחדים בהקשר של הצפנת אל-גמאל
בואו נדון בשאלה למה אנחנו רוצים חבורה עם תכונות מסוימות. אנחנו רוצים שיהיה קשה למצוא את הלוגריתם בחבורה, נכון? אם $g$ הוא יוצר בחבורה מסדר $p$, אני צריך לעבור על כל איברי החבורה עד שאתקל במה שאני מחפש.
אני יודע שבחבורה יכולות להיות תת-חבורות, ואם אבחר איבר מתת-חבורה קטנה, אוכל למצוא את החזקות שלו בקלות יחסית. לכן, אני מעוניין בתת-חבורות גדולות.
מספרים ראשוניים בטוחים
אחד הסוגים החשובים ביותר בהקשר של הצפנת אל-גמאל הוא “מספר ראשוני בטוח” (Safe prime). מספר ראשוני $p$ מוגדר כבטוח כאשר מתקיים:
\[p = 2q + 1\]כאשר $q$ הוא גם מספר ראשוני. המספר $q$ מכונה “מספר ראשוני של סופי ז’רמן” (Sophie Germain prime), על שם המתמטיקאית הצרפתייה המפורסמת.
דוגמאות למספרים ראשוניים בטוחים:
- $p = 11$ (כאשר $q = 5$, מכיוון ש-$11 = 2 \cdot 5 + 1$)
- $p = 23$ (כאשר $q = 11$, מכיוון ש-$23 = 2 \cdot 11 + 1$)
- $p = 47$ (כאשר $q = 23$, מכיוון ש-$47 = 2 \cdot 23 + 1$)
המבנה האלגברי של החבורה $\mathbb{Z}_p^*$
כאשר בוחרים מספר ראשוני בטוח $p = 2q + 1$, מתקבלת חבורה מיוחדת מאוד בעלת תכונות אלגבריות יעילות. החבורה המולטיפליקטיבית $\mathbb{Z}_p^*$ (המורכבת מכל המספרים מ-1 עד $p-1$ תחת פעולת הכפל מודולו $p$) מקבלת מבנה מסודר ופשוט יחסית.
במבנה זה, הסדר של כל איבר בחבורה יכול להיות רק אחד מארבעה ערכים:
- סדר 1: רק האיבר 1
- סדר 2: רק האיבר $p-1$ (שווה ערך ל-$-1 \mod p$)
- סדר $q$: חלק מהאיברים הנותרים
- סדר $2q$ (שהוא $p-1$): שאר האיברים
חשיבות היוצרים בהצפנת אל-גמאל
בהצפנת אל-גמאל, הפרמטר הבסיסי ביותר הוא “יוצר” (Generator) של החבורה $\mathbb{Z}_p^*$. יוצר הוא איבר $g$ שמקיים את התכונה הבאה: מחזוריות הכפל החוזר של $g$ בעצמו (מודולו $p$) יוצרת את כל איברי החבורה.
כאשר $p$ הוא מספר ראשוני בטוח, ניתן להוכיח שמספר היוצרים בחבורה הוא:
\[\phi(p-1) = \phi(2q) = \phi(2) \cdot \phi(q) = 1 \cdot (q-1) = q-1\]כלומר, בערך מחצית מאיברי החבורה הם יוצרים, מה שמקל מאוד על מציאתם.
זיהוי יוצרים באופן יעיל
הודות למבנה המיוחד של החבורה במקרה של מספר ראשוני בטוח, קיים קריטריון פשוט ויעיל לזיהוי איבר $g$ כיוצר:
$g$ הוא יוצר אם ורק אם $g^q \neq 1 \mod p$
נזכיר כי תנאי זה בודק שהאיבר $g$ אינו מסדר $q$, ומכיוון שהאפשרויות היחידות הנותרות (מלבד האיברים 1 ו-$p-1$ שקל לזהות) הן סדר $2q = p-1$, הרי שאיבר העומד בתנאי זה חייב להיות יוצר.
יישום בפרוטוקול אל-גמאל
במערכת ההצפנה של אל-גמאל, תהליך יצירת המפתחות כולל את השלבים הבאים:
- בחירת מספר ראשוני בטוח $p = 2q + 1$ (באמצעות האלגוריתם שתואר)
- מציאת יוצר $g$ בחבורה $\mathbb{Z}_p^*$ (באמצעות הקריטריון שתואר)
- בחירת מספר פרטי $x$ מהתחום ${1, 2, \ldots, p-2}$
- חישוב המפתח הציבורי $y = g^x \mod p$
המפתח הפרטי הוא $x$, והמפתח הציבורי הוא השלשה $(p, g, y)$.
לסיכום, השימוש במספרים ראשוניים בטוחים מעניק יתרונות משמעותיים למערכת ההצפנה של אל-גמאל:
- המבנה המתמטי הפשוט של החבורה מאפשר יצירת מפתחות ביעילות
- התכונות האלגבריות מספקות עמידות גבוהה כנגד שיטות קריפטואנליזה ידועות
- המבנה המיוחד מקל על מציאת יוצרים, שהם מרכיב קריטי במערכת
הבנת התכונות המתמטיות הייחודיות של מספרים ראשוניים בטוחים והחבורות המתאימות להם היא מפתח להבנה מעמיקה של עקרונות הפעולה והאבטחה של הצפנת אל-גמאל.