סיכומי קריפטוגרפיה - RSA
הקדמה
כתבתי את הפוסט הזה כדי לחזור על החומר שלמדתי בקורס ״מבוא לקריפטוגרפיה״. אם אתם מוצאים אי-דיוקים, או אם יש לכם שאלות או רעיונות, מוזמנים ליצור קשר ולפנות אלי דרך האתר.
RSA
RSA הוא אלגוריתם הצפנה אסימטרי (עם מפתח פומבי) שפותח על ידי רון ריבסט, עדי שמיר ולאונרד אדלמן ב-1977. האלגוריתם מבוסס על הקושי של פירוק מספרים גדולים לגורמים ראשוניים.
עקרונות היסוד של RSA:
- יצירת מפתחות:
- בוחרים שני מספרים ראשוניים גדולים $p$ ו-$q$
- מחשבים את המודולוס $n$ בעזרת המכפלה שלהם $n = p \times q$
- מחשבים את פונקציית אוילר $\phi(n) = (p-1) \times (q-1)$
- בוחרים מספר $a$ כך ש-$1 < a < \phi(n)$ ו-$gcd(a, \phi(n)) = 1$
- מחשבים $b$ כך ש-$a \times b \equiv 1 \pmod{\phi(n)}$ - כלומר $b$ הוא ההופכי המודולרי של $a$ במודולו $\phi(n)$
- המפתח הפומבי הוא $(n, b)$, והמפתח הפרטי הוא $(n, a)$
-
הצפנה: בהינתן הודעה $m$, מחשבים את ההודעה המוצפנת $m^b \equiv c \pmod{n}$
- פענוח: בהינתן הודעה מוצפנת $c$, מחשבים את המספר שמייצג את ההודעה המקורית $c^a \equiv m \pmod{n}$
RSA משמש בעיקר להצפנת מפתחות עבור אלגוריתמים סימטריים ולא להצפנת הודעות ארוכות ישירות, זאת בשל יעילות נמוכה יחסית:
- ההודעה $m$ היא בעצם מספר שמייצג כל תוכן $M$. אם למשל ההודעה היא ״שלום״, אני יכול להמיר את המילה למספר על ידי קידוד של כל תו (למשל, ASCII או UTF-8) ואז לחבר את המספרים. לדוגמה, ״שלום״ ב-UTF-8 היא
0xD7A9D7A8D7B4D799.
“רוב הזמן כשאתה מצפין משהו ב-
RSA, אתה מצפין מפתח סימטרי, אבל לא מצפינים באמת ב-RSAשום דבר חוץ ממפתח.”“תחשב שיש לך קובץ של ג’יגה. מפתח של
RSAזה אלף ביטים. מה אתה עושה? תפרק את זה. זה מטורף, זהPublic Key, זה פעולה מאוד לא יעילה.”
 |
|---|
| תהליך הצפנה ופענוח ב-RSA |
 |
|---|
| דוגמה להצפנה ופענוח ב-RSA |
הסברים טכניים
החלק הבא ינסה להסביר כמה יסודות שיכולים לעזור להבין למה:
\[e(d(m)) \equiv m \pmod{n}\]הקדמה - מודולוס, $\mathbb{Z}_m^*$ וצופן אפיני
צופן אפיני מבוסס על מפתח שמורכב מזוג סדור של מספרים $K=(a, b)$. הצופן עובד על אלפבית בגודל $m$ (למשל, אלפבית אנגלי בגודל 26). פונקציית ההצפנה היא $e(x) = (a \cdot x + b) \mod m$, כאשר $x$ הוא המספר המייצג את התו באלפבית. פונקציית הפענוח היא $d(y) = a^{-1} \cdot (y - b) \mod m$, כאשר $y$ הוא המספר המייצג את התו המוצפן באלפבית.
לא כל $a$ יכול לשמש כמפתח. כדי שהצופן יעבוד, $a$ חייב להיות זר יחסית ל-$m$, כלומר $\gcd(a, m) = 1$. אחרת, ייתכנו כמה פירושים לאותו טקסט מוצפן, ופונקציית ההצפנה לא תעבוד (כי היא לא חד חד ערכית).
בספר הלימוד סימנו את קבוצת הערכים שהמחלק המשותף הגדול ביותר שלם ושל $m$ הוא 1 ב-$\mathbb{Z}_m^*$:
\[\mathbb{Z}_m^* = \{x \in \mathbb{Z}_m | \gcd(x, m) = 1\}\]הגודל של הקבוצה הזו הוא $\phi(m)$, כאשר $\phi$ היא פונקציית אוילר. פונקציית אוילר מחזירה את מספר המספרים הקטנים מ-$n$ שאין להם מחלקים משותפים עם $n$. לדוגמה, $\phi(6) = 2$, כי 1 ו-5 הם היחידים הקטנים מ-6 שאין להם מחלקים משותפים עם 6.
מציאת מחלק משותף מקסימלי או הופכי מודולרי
חבורה היא מבנה אלגברי שכולל קבוצה ופעולה בינארית.
החבורה $\mathbb{Z}_n^*$ היא קבוצת כל השאריות מודולו $n$ הזרות ל-$n$ (כלומר, כל המספרים מ-1 עד $n-1$ שאין להם מחלקים משותפים עם $n$), עם פעולת כפל מודולו $n$. אפשר להוכיח שבחבורה כזו, אם $b$ זר ל-$n$, אז יש ל-$b$ איבר הופכי מודולו $n$ שגם הוא בחבורה. כלומר, אם $b$ הוא איבר בחבורה, אז קיים $b^{-1} $ שגם הוא בחבורה (זר ל-$n$) כך ש-$b \cdot b^{-1} \equiv 1 \pmod{n}$.
כדי לחשב את המחלק המשותף המקימסלי של שני מספרים gcd(b,n), וכדי לחשב את ההופכי המודולרי b^{-1} mod n במקרה ששני המספרים זרים זה לזה, אפשר להשתמש באלגוריתם אוקלידס. מצורף למטה מימוש של האלגוריתם בפייתון.
| i | r | q | s | t |
|---|---|---|---|---|
| 0 | r₀=154 | s₀= 1 | t₀ = 0 | |
| 1 | r₁= 84 | q₁= 1 | s₁= 0 | t₁ = 1 |
| 2 | r₂= 70 | q₂= 1 | s₂= 1 | t₂ = -1 |
| 3 | r₃= 14 | q₃= 5 | s₃= -1 | t₃ = 2 |
חבורות מעגליות ויוצרים
חבורה היא מעגלית (cyclic) אם יש לה יוצר. יוצר הוא איבר שאם נעלה אותו בכל החזקות האפשריות, נקבל את כל איברי החבורה. כדי לחזור לאיבר הניטרלי (1), אנחנו צריכים להעלות את היוצר בחזקת $p-1$, כלומר לעבור את כל הסיבוב עד שחזרנו ל-1. כל חזקה קטנה יותר לא תניב את האיבר הניטרלי.
נבדוק דוגמאות:
\[\begin{aligned} 2^0 = 1 & \equiv 1 \pmod{5} \\ 2^1 = 2 & \equiv 2 \pmod{5} \\ 2^2 = 4 & \equiv 4 \pmod{5} \\ 2^3 = 8 & \equiv 3 \pmod{5} \\ 2^4 = 16& \equiv 1 \pmod{5} \end{aligned}\]אנחנו נעבוד עם חבורות ציקליות מהצורה $\mathbb{Z}_P^*$, כלומר חבורות של מספרים מודולו $P$, כאשר $P$ הוא מספר ראשוני (מספרים שלמים מ-1 עד $P-1$).
לדוגמה, החבורה $\mathbb{Z}_5^*$ היא \(\{1, 2, 3, 4\}\) עם פעולת כפל מודולו 5. החבורה הזאת היא מעגלית, כי כל איבר מתקבל כחזקה של 2, כמו שהראנו למעלה. חבורה גדולה יותר היא \(\mathbb{Z}_{17}^* = \{1, 2, 3, \ldots, 16\}\) עם פעולת כפל מודולו 17. גם כאן החבורה היא מעגלית, כי כל איבר מתקבל כחזקה של 3:
| $\mathbb{Z}_{17}^*$ | $3^k \mod 17$ |
|---|---|
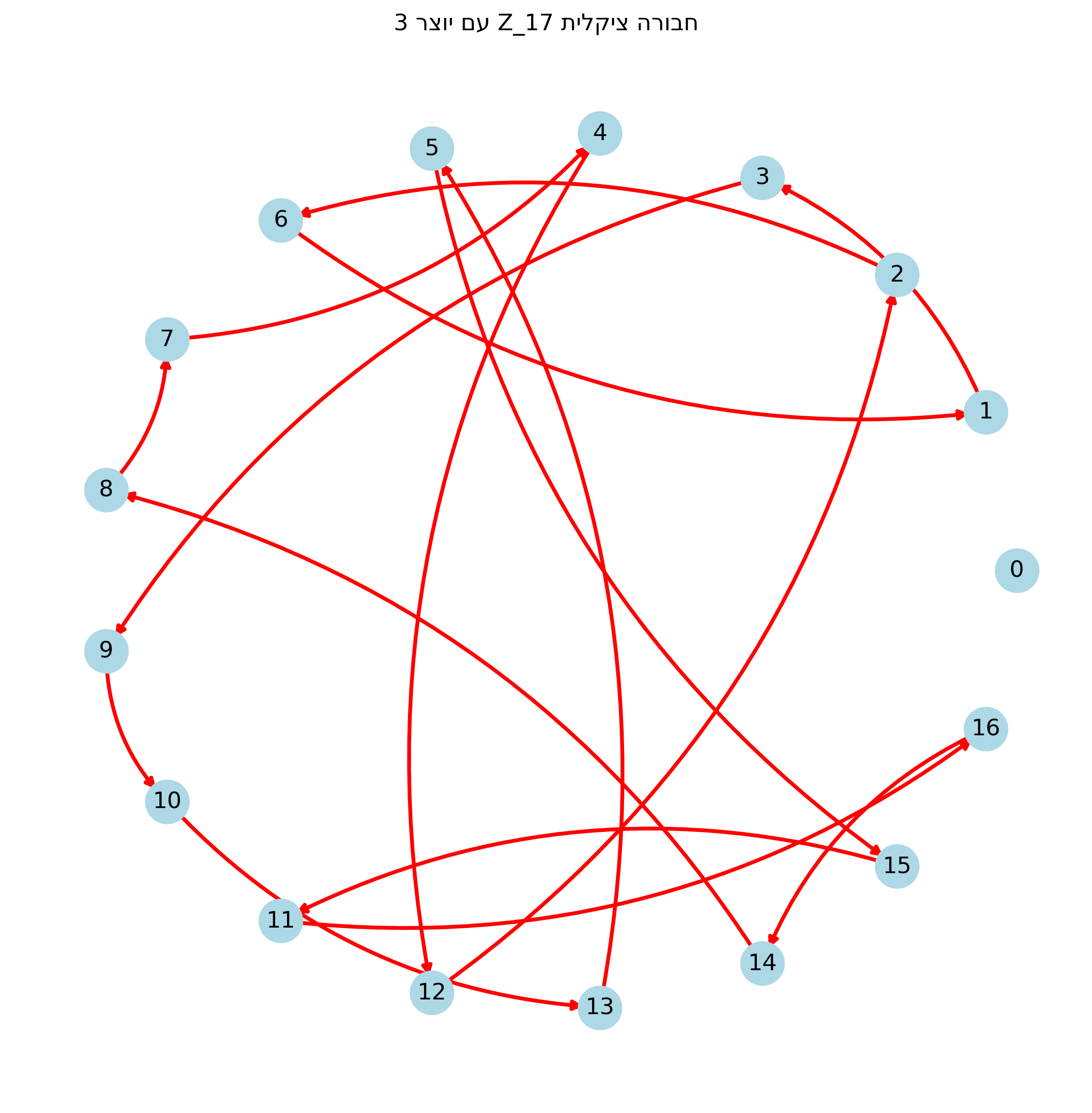 | 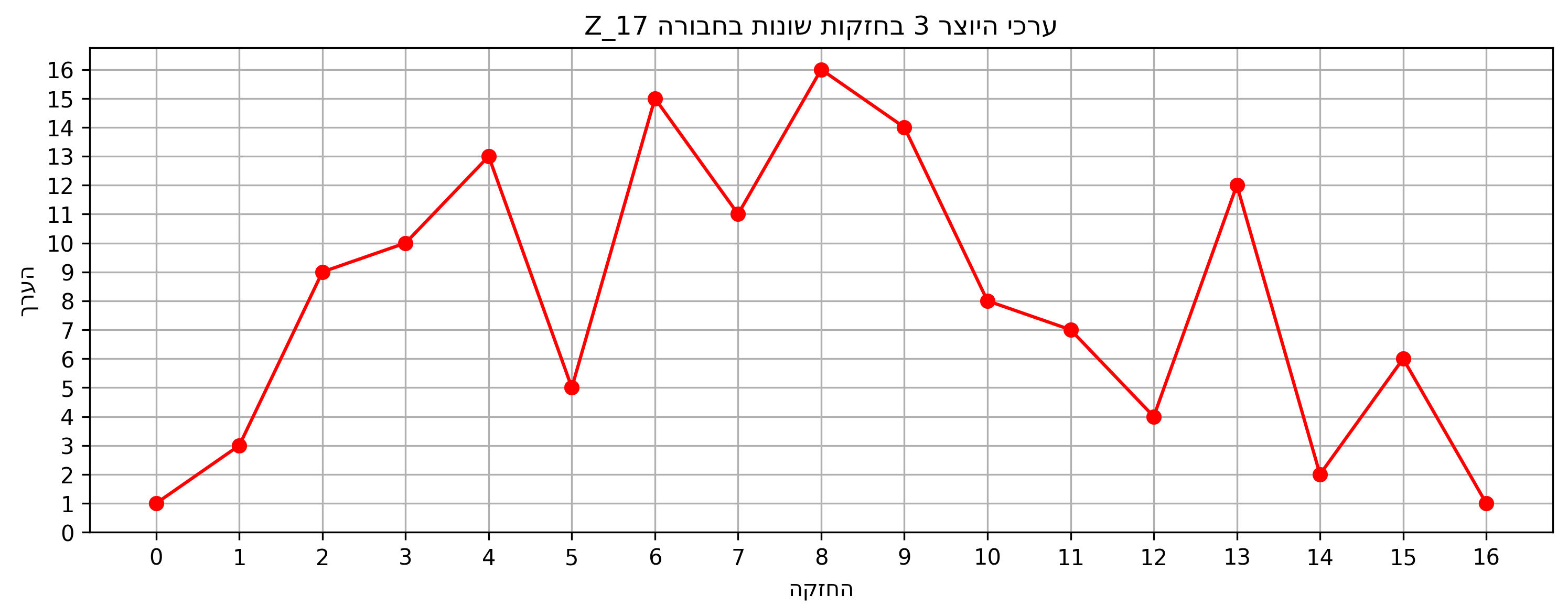 |
הערה: הדרישה ש-$P$ יהיה ראשוני הכרחית כדי להבטיח שהחבורה $\mathbb{Z}_P^* $ תקיים תכונות מסוימות, למשל, שבהכרח קיים לה לפחות יוצר אחד. אני לא מרחיב כאן על הנושא, או על מושג החבורה באופן כללי. מוזמנים לקרוא בויקיפדיה.
משפט למציאת יוצרים
אפשר לנסח את התכונה ‘אם נעלה אותו בכל החזקות האפשריות נקבל את כל איברי החבורה’ גם באופן אחר: איבר יוצר הוא איבר שהסדר שלו שווה לסדרר של החבורה. אם $g$ הוא יוצר של החבורה $\mathbb{Z}_P^*$, אז כל איבר $a \in \mathbb{Z}_P^*$ ניתן לכתיבה בצורה $a = g^k \mod P$ עבור $k=0,1,\ldots,P-2$.
מציאת היוצרים של חבורה מעגלית בצורה נאיבית נעשית על ידי בחינת כל איבר $g$ בחבורה ובדיקת החזקות שלו. אם $g^k \mod P$ נותן את כל האיברים בחבורה, אז $g$ הוא יוצר. במקרה שהחבורה גדולה מאוד, בדיקה כזאת לעיתים לא ישימה. למקרה כזה ניתן להיעזר במשפט הבא, שמתבסס על התכונה שסדר של יוצר שווה לסדר החבורה. המשפט מופיע בניסוח דומה כ-Theorem 6.8 בספר Cryptography: Theory and Practice של R. Stinson (עמוד 196).
יהי $P$ ראשוני. נפרק את $P-1$ ל-$n$ גורמים ראשוניים:
\[P - 1 = P_1^{e_1} \cdot P_2^{e_2} \cdot \ldots \cdot P_n^{e_n}\]$g$ הוא יוצר של החבורה $\mathbb{Z}_P^*$ אם ורק אם לכל גורם ראשוני $P_i$ של $P-1$ מתקיים:
\[g^{\frac{P-1}{P_i}} \not\equiv 1 \pmod{P}\]
כלומר, במקום לבדוק את כל החזקות של $g$, אנחנו יכולים לבדוק רק את החזקות של $g$ שמתקבלות על ידי חלוקת $P-1$ בגורמים הראשוניים של $P-1$.
נבדוק את המשפט הזה עם דוגמה מספרית: נניח שהחבורה היא $\mathbb{Z}_{17}^*$, כלומר $P=17$. אז $P-1=16$, נבדוק אם 3 הוא יוצר של החבורה:
- סדר החבורה הוא 16, כלומר $P-1=16$, כי $P$ הוא ראשוני.
-
ל-$16$ יש רק גורם ראשוני אחד, שהוא 2:
\[16=2\times 2\times 2 \times 2 \rightarrow P_1=2\] -
נחשב את $g^{\frac{P-1}{P_1}}$:
\[g^{\frac{P-1}{P_1}} = 3^{\frac{16}{2}} = 3^8 = 16 \mod 17\]
הוכחה
-
כיוון ראשון: אם $g$ יוצר, אז $g^{\frac{P-1}{P_i}} \not\equiv 1 \pmod{P}$ לכל $i$
נניח ש-$g$ הוא יוצר של החבורה $\mathbb{Z}_P^*$. לפי הגדרה, סדר של יוצר שווה לסדר החבורה. סדר החבורה $\mathbb{Z}_P^*$ הוא $\phi(P) = P-1$ (כאשר $\phi$ היא פונקציית אוילר).
נניח בשלילה שקיים $i$ כך ש-$g^{\frac{P-1}{P_i}} \equiv 1 \pmod{P}$. משמעות הדבר היא שסדר האיבר $g$ חייב לחלק את $\frac{P-1}{P_i}$ (שהוא מספר קטן מ-$P-1$). אבל אז $g$ אינו יוצר, כי סדרו קטן מסדר החבורה. סתירה להנחה שלנו.
לכן, אם $g$ יוצר, בהכרח $g^{\frac{P-1}{P_i}} \not\equiv 1 \pmod{P}$ לכל $i$.
-
כיוון שני: אם עבור כל $i$ מתקיים $g^{\frac{P-1}{P_i}} \not\equiv 1 \pmod{P}$, אז $g$ יוצר
נשתמש במשפט לגראנז’ הקובע כי סדר כל איבר בחבורה מחלק את סדר החבורה.
נסמן את סדר האיבר $g$ ב-$D$. אנו יודעים ש-$D$ חייב לחלק את סדר החבורה $P-1$.
כיוון ש-$P-1 = P_1^{e_1} \cdot P_2^{e_2} \cdot \ldots \cdot P_n^{e_n}$, כל מחלק של $P-1$ (כולל $D$) חייב להיות בצורה:
\[D = P_1^{\alpha_1} \cdot P_2^{\alpha_2} \cdot \ldots \cdot P_n^{\alpha_n}\]כאשר $0 \leq \alpha_i \leq e_i$ לכל $i$.
נניח בשלילה ש-$D < P-1$. אז קיים לפחות ערך $j$ אחד כך ש-$\alpha_j < e_j$. נגדיר:
\[D' = \frac{P-1}{P_j} = P_1^{e_1} \cdot \ldots \cdot P_j^{e_j-1} \cdot \ldots \cdot P_n^{e_n}\]מכיוון ש-$\alpha_j < e_j$, נובע ש-$D$ מחלק את $D’$ (שכן כל חזקות הגורמים הראשוניים ב-$D$ קטנות או שוות לחזקות המתאימות ב-$D’$).
לכן, $g^{D’} \equiv (g^D)^{D’/D} \equiv 1^{D’/D} \equiv 1 \pmod{P}$, כלומר $g^{\frac{P-1}{P_j}} \equiv 1 \pmod{P}$. אבל זה סותר את הנתון שלנו.
לפיכך, ההנחה $D < P-1$ שגויה, ומכאן נובע ש-$D = P-1$, כלומר $g$ הוא יוצר של החבורה.
משפט לגראנז’, משפט אוילר והסדר של איבר
-
סדר של קבוצה: מספר האיברים בקבוצה. במקרה שהקבוצה היא $\mathbb{Z}_n^*$, הסדר שלה הוא $|\mathbb{Z}_n^*| = \phi(n)$ לפי הגדרה (פונקציית אוילר מחזירה את מספר המספרים הקטנים מ-$n$ שאין להם מחלקים משותפים עם $n$, שאלה בדיוק איברי הקבוצה $\mathbb{Z}_n^*$).
-
סדר של איבר: המספר הקטן ביותר $d$ כך ש-$g^d \equiv 1 \pmod{n}$.
- לדוגמה, אם $g=2$ ו-$n=5$, אז $2^4 \equiv 1 \pmod{5}$, ולכן הסדר של 2 הוא 4.
- אם $g=3$ ו-$n=7$, אז $3^6 \equiv 1 \pmod{7}$, ולכן הסדר של 3 הוא 6.
-
משפט לגראנז’: אם $G$ חבורה סופית ו-$g \in G$, אז הסדר של $g$ מחלק את סדר החבורה $|G|$. ברישום פורמאלי: $ord(g) \mid |G|$
-
מסקנה חשובה לחבורה $\mathbb{Z}_n^*$: אם $g \in \mathbb{Z}_n^*$, אז: $g^{\phi(n)} \equiv 1 \pmod{n}$
המסקנה האחרונה (משפט אוילר) נובעת ממשפט לגראנז’. נניח ש-$g$ הוא איבר בחבורה $\mathbb{Z}_n^*$, כלומר $g \in \mathbb{Z}_n^*$. אז קיים $d$ שלם כך ש:
\[g^{d} \equiv 1 \pmod{n}\]זהו הסדר של $g$. לפי משפט לגראנז’, הסדר של $g$ מחלק את סדר החבורה $|\mathbb{Z}_n^* | = \phi(n)$. כלומר, קיים $k$ שלם כך ש:
\[d \cdot k = \phi(n)\]נפשט את הביטוי $g^{\phi(n)}$ ונקבל:
\[g^{\phi(n)} = g^{d \cdot k} \equiv (g^d)^k \equiv 1^k \equiv 1 \pmod{n}\]אז למה RSA עובד?
\[d\left(e \left(m\right) \right) = d\left(m^b \pmod{n} \right) = m^{b \cdot a} \pmod{n} \overset{?}{\equiv} m \pmod{n}\]בגלל ש-$a\cdot b \equiv 1 \pmod{\phi(n)}$ נוכל לרשום את $a \cdot b$ כמכפלה של מספר שלם $t$ ב-$\phi(n)$ ועוד שארית 1:
\[\begin{aligned} m^{a \cdot b} &\equiv m^{1 + t \cdot \phi(n)} \pmod{n} \\ &\equiv m^1 \cdot m^{t \cdot \phi(n)} \pmod{n} \\ &\equiv m^1 \cdot (m^{\phi(n)})^t \pmod{n} \end{aligned}\]אם $m$ זר גם ל$q$ וגם ל$p$ אז $m\in \mathbb{Z}_n^*$ שכל $gcd(m, n) = 1$, אז לפי משפט אוילר $m^{\phi(n)} \equiv 1 \pmod{n}$, ולכן:
\[\begin{aligned} m^{a \cdot b} &\equiv m^1 \cdot (m^{\phi(n)})^t \pmod{n} \\ &\equiv m^1 \cdot 1^t \pmod{n} \\ &\equiv m^1 \cdot 1 \pmod{n} \\ &\equiv m \pmod{n} \end{aligned}\]אם $m$ מתחלק בשניהם אז בהכרח $m=0$ (או $m=n$), ולכן $m^{a \cdot b} \equiv 0 \pmod{n}$.
אם $m$ מתחלק רק באחד מהם, אפשר להגיע לתוצאה דומה.
ניתוח אבטחת הצפנת RSA
שימוש במעריך פומבי קטן והעברת מסר קצר
נבחן את אבטחת RSA באמצעות דוגמה:
לבוב יש מפתח RSA עם מודולוס $n$ בגודל שנחשב בטוח של 2048 ביט ומעריך פומבי $e = 3$. אליס רוצה לשלוח לבוב קובץ גדול, וכיוון שיותר יעיל להשתמש בהצפנה סימטרית, היא:
- מגרילה מפתח $K$ להצפנת
AESבגודל128ביט - שולחת לבוב את $K$ מוצפן ב-
RSAבאופן הבא: $K^e \equiv C \bmod n$ - שולחת את הקובץ מוצפן ב-
AESעם המפתח $K$
לפענוח, בוב:
- מחלץ את $K$ על ידי חישוב $C^d \equiv K \bmod n $
- מפענח את הקובץ המוצפן באמצעות $K$
השאלה: האם ההצפנה הזאת אכן בטוחה?
ניתוח
התשובה היא לא. למרות ש-RSA נחשבת בטוחה כאשר המודולוס מספיק גדול (2048 ביט), יש בעיה בשימוש שתואר:
כאשר מצפינים מפתח בגודל 128 ביט באמצעות RSA עם מעריך $e = 3$ ומודולוס של 2048 ביט, המספר $K^3$ עדיין קטן מ-$n$. לכן, לא מתבצעת רדוקציה מודולרית, ואפשר פשוט לחשב את השורש הקובי של $C$ כדי לקבל את $K$.
המחשה מתמטית:
- $K$ הוא מספר של
128ביט - $K^3$ הוא בערך $128 \times 3 = 384$ ביט
- מאחר ש-384 < 2048, לא מתבצעת רדוקציה מודולרית
- לכן $C = K^3$ (ללא חישוב מודולו)
- תוקף יכול פשוט לחשב $\sqrt[3]{C}$ ולקבל את $K$
הפתרון: להוסיף ריפוד (padding) אקראי למסר לפני ההצפנה ב-RSA, כך שהמסר המועלה בחזקה $e$ יהיה גדול מספיק ותתבצע הרדוקציה המודולרית.
קוד פייתון למימוש התקיפה
import random
class RSA:
def __init__(self, p, q):
self.n = p * q
self.public_key = (n, b)
self.private_key = (n, a)
#TODO: implament RSA
n = random.getrandbits(2047) | (1 << 2047)
k = random.getrandbits(127) | (1 << 127)
e = 3.0
C = k ** e
def cube_root(c):
return c ** (1.0 / e)
evil = round(cube_root(C))
print(f'k = {k}')
print(f'C = {C} (k^e mod N)')
print(f"C**1/3 = {evil}")
למה חזקה היא פעולה קשה?
חזקה מודולרית נחשבת לפעולה קשה בגלל שאין לה את תכונת המונוטוניות. אם היית מעלה ערך בחזקה מעל הממשיים, היית יכול להתקרב באופן מהיר לערך שאתה מחפש בגלל שיש מונוטוניות. אבל במודולו, אתה לא יכול לעשות עריכה במדבר - אתה לא יכול להשתמש בחיפוש בינארי או בטכניקות דומות, כי יש קפיצות בערכים ואין הבטחה של מונוטוניות.
בפעולות מודולריות, אין אפשרות לנצל תכונות מונוטוניות כדי להתקרב לפתרון, וזה מה שהופך את בעיית הלוגריתם הדיסקרטי (להלן בחלק על אל-גמל, אבל גם רלוונטי לפירוק לגורמי) לקשה.
אותה הודעה, מודולוס משותף
אחד החסרונות של שימוש לא זהיר ב-RSA נובע ממצב שבו שני נמענים חולקים את אותו מודולוס $N$, אך משתמשים באקספוננט שונה (כלומר, מפתח פומבי שונה).
נניח שאנחנו שולחים את אותה הודעה $M$ לשני נמענים שונים:
- בוב 1 משתמש במפתח הפומבי $(N, B_1)$
- בוב 2 משתמש במפתח הפומבי $(N, B_2)$
- ההצפנה מתבצעת כך:
- $C_1 = M^{B_1} \mod N$
- $C_2 = M^{B_2} \mod N$
נניח שיריב יודע ש-$C_1$ ו-$C_2$ הם הצפנות של אותה הודעה $M$, וש-$\gcd(B_1, B_2) = 1$ (כלומר, האקספוננטים זרים זה לזה — תנאי שניתן לבדוק בקלות בעזרת אלגוריתם אוקלידס).
האם היריב יכול לחשוף את $M$?
כן. הוא יכול להשתמש באלגוריתם אוקלידס המורחב כדי למצוא מקדמים של $B_1$ ו-$B_2$ שמספקים:
\[S \cdot B_1 + T \cdot B_2 = 1\](כיוון שהמספרים זרים, קיימים בהכרח $S, T \in \mathbb{Z}$ שמקיימים את הזהות הזאת.)
כעת, היריב יכול לחשב:
\[M^{S \cdot B_1 + T \cdot B_2} \equiv M \pmod{N}\]באופן מעשי, זה מתבצע על-ידי:
\[M = (C_1)^S \cdot (C_2)^T \mod N\]שים לב: אם אחד מהמקדמים $S$ או $T$ שליליים, יש לחשב הופכי מודולרי של $C_1$ או $C_2$ בהתאמה (לדוגמה: $C_1^{-1}$).
סיכום הנזק
- התוקף לא צריך לדעת את המפתח הפרטי של אף אחד.
- ברגע שהוא יודע ששני קידודים הם של אותה הודעה ושיש להם מודולוס זהה ואקספוננטים זרים — הוא יכול לחלץ את ההודעה $M$ ישירות.
מה הלקח?
לעולם אל תשתף את אותו מודולוס $N$ בין שני משתמשים שונים. כל משתמש ב-RSA אמור ליצור לעצמו זוג מפתחות נפרד, עם פרמטרים $p, q$ שונים, שמהם נגזר $N$ שונה.
זו טעות נפוצה במיוחד במערכות שבהן רוצים לחסוך בחישוב — למשל, כאשר צד אחד (כמו embedded device) מייצר רק את המפתח הפומבי ואותו משתפים בין כמה גורמים. אבל שיתוף מודולוס הוא סיכון חמור מבחינת אבטחה.
חולשה של הצפנה הומומורפית
יש מערכות הצפנה שמקיימות תכונות הומומורפיות:
- הומומורפיזם כפלי (
Multiplicative Homomorphism):- $E(x) \cdot E(y) = E(x \cdot y)$
- RSA היא מערכת הומומורפית כפלית (ראו הוכחה להלן)
- הומומורפיזם חיבורי (
Additive Homomorphism):- $E(x) + E(y) = E(x + y)$
- הצפנה הומומורפית מלאה (
Fully Homomorphic Encryption - FHE):- מערכת שהיא הומומורפית גם לכפל וגם לחיבור
- מאפשרת לבצע כל פעולה חישובית על מידע מוצפן
המרצה: “עד 2009 לא ידענו לעשות הצפנה הומומורפית מלאה, עד שקרייג ג׳נטרי הציע סכמה. אחרי זה יצאו סכמות נוספות שהן לא מסובכות להבנה אבל עדיין קשות ליישום. רעיונות מדהימים של RLWE וגברות הרעש, לא ניכנס לזה פה, זה באמת חומר מאוד מתקדם.”
שימושים פוטנציאליים:
- שירותי ענן שיכולים לעבד מידע מוצפן בלי לדעת מה תוכנו
- חיפוש במסד נתונים מוצפן
- עיבוד מידע רפואי רגיש ללא חשיפתו
המרצה הסביר את ההשלכות המעשיות של הצפנה הומומורפית מלאה:
“תחשבו שהמיילים שלכם, שהיום יושבים בענן, יהיו מוצפנים והענן לא יוכל לקרוא אותם, אבל עדיין יוכל לחפש עבורכם במיילים ולהחזיר תוצאות. הוא יוכל לעשות חישובי אקסל, להוציא דוחות, והכל בלי לדעת על מה הוא מחשב. זה פיצוץ!”
אבטחה סמנטית (Semantic Security)
אבטחה סמנטית מוגדרת כיכולת של מערכת הצפנה למנוע מתוקף ללמוד מידע כלשהו על ההודעה המקורית מההודעה המוצפנת.
הגדרה שקולה: “אי יכולת להבחין” (Indistinguishability)
דוגמה להגדרה:
- יש לנו הודעות $X_0$ ו-$X_1$
- בוחרים באקראי $b \in {0, 1}$ ומצפינים את $X_b$
- נותנים למתקיף את ההצפנה $E(X_b)$
- אם המתקיף אינו יכול לנחש את $b$ בסיכוי גדול מ-50%, המערכת היא סמנטית בטוחה
RSA אינה סמנטית בטוחה כי הצפנת אותה הודעה תמיד תניב את אותה תוצאה. לעומת זאת, מערכות שמכניסות אקראיות בתהליך ההצפנה (כמו אל-גמאל) יכולות להיות סמנטית בטוחות.
הוכחת הומומורפיזם כפלי ב-RSA
נוכיח שכפל של הצפנות RSA שווה להצפנה של כפל הטקסטים המקוריים:
נסמן את $E(x)$ בתור ההצפנה של טקסט מקור $x$, כלומר $E(x) = x^b \mod n$ ב־RSA.
אם יש לנו שני טקסטים מקוריים $x$ ו־$y$, ההצפנות שלהם ב־RSA יהיו $E(x)$ ו־$E(y)$, כלומר:
כפל ההצפנות האלו נותן:
\[E(x) \cdot E(y) = (x^b \mod n) \cdot (y^b \mod n)\]לפי חוקי חשבון מודולרי (כפל בחזקות), אפשר לרשום זאת כך:
\[= (x^b \cdot y^b) \mod n \\ = (xy)^b \mod n\]וזו בדיוק ההצפנה של מכפלת הטקסטים המקוריים $x$ ו־$y$, כלומר:
\[E(xy)\]לכן מתקיים:
\[E(x) \cdot E(y) = E(xy)\]באופן כללי, לדוגמה:
\[E(x) \cdot E(y) \cdot E(x) = E(x) \cdot E(x) \cdot E(y) = (x^b \mod n)(x^b \mod n)(y^b \mod n) = E(x^2 y)\]דוגמה לניצול של הומומורפיזם כפלי
- נניח שתוקף יודע את ההצפנה של $x$, כלומר $E(x)$.
- הוא יכול לחשב $E(x^2) = E(x)^2$, בלי לדעת את $x$.
- אם הוא מנחש $x$ אפשרי, הוא פשוט משווה $E(x)$ למה שיש לו – התקפת ניחוש (Guessing Attack).
דוגמה: אם המשתמש שלח את הסכום $10, והתוקף יודע שהאפשרויות הן רק {5, 10, 20}, הוא יכול לחשב את $E(5), E(10), E(20)$ ולזהות את הערך הנכון – מבלי לפענח.
שורשי קוביה (שורש שלישי) במבנה אלגברי והקשר להצפנת RSA
נגדיר את הנתונים:
- $p, q$ הם מספרים ראשוניים אי-זוגיים שונים
- 3 אינו מחלק את $p-1$ וגם אינו מחלק את $q-1$
- $n = pq$
השאלה: כמה איברים $a$ בחבורה $Z_n^*$ מקיימים שקיים עבורם $b$ כך ש-$b^3 \equiv a \pmod{n}$?
פתרון הבעיה
-
לפי משפט השארית הסיני, $Z_n^* \cong Z_p^* \times Z_q^*$
- נבחן את הפונקציה $f(x) = x^3$ ב-$Z_p^*$:
- $Z_p^*$ היא חבורה מחזורית מסדר $p-1$
- מספר האיברים $x$ המקיימים $x^3 \equiv 1 \pmod{p}$ הוא $\gcd(3, p-1)$
- מכיוון ש-3 אינו מחלק את $p-1$, מתקיים $\gcd(3, p-1) = 1$
- לכן הפונקציה $f$ היא חד-חד-ערכית ועל
- המסקנה: לכל איבר ב-$Z_p^*$ יש בדיוק שורש קוביה אחד
-
באופן זהה, לכל איבר ב-$Z_q^*$ יש בדיוק שורש קוביה אחד
- לכן, כל איבר ב-$Z_n^*$ הוא שורש קוביה של איבר אחר
התשובה: מספר האיברים המבוקשים הוא
\[|Z_n^*| = \phi(n) = (p-1)(q-1)\]הקשר להצפנת RSA
הצפנת RSA פועלת בדיוק באותה מסגרת מתמטית:
-
בסיס מתמטי: RSA פועל בחבורה $Z_n^*$ כאשר $n = pq$
- מפתחות RSA:
- מפתח ציבורי: $(n, e)$ כאשר $e$ הוא המעריך להצפנה
- מפתח פרטי: $d$ שמקיים $ed \equiv 1 \pmod{\phi(n)}$
- $\phi(n) = (p-1)(q-1)$ בדיוק כפי שחישבנו
- הצפנה ופענוח:
- הצפנה: $c \equiv m^e \pmod{n}$
- פענוח: $m \equiv c^d \pmod{n}$
- המקרה $e=3$:
- כאשר $e=3$, ההצפנה היא $c \equiv m^3 \pmod{n}$
- הבעיה שפתרנו בדיוק בוחנת מתי יש פתרון יחיד למשוואה $x^3 \equiv a \pmod{n}$
- התנאים על $p$ ו-$q$ (ש-3 אינו מחלק את $p-1$ או $q-1$) מבטיחים שלכל הודעה מוצפנת יש פתרון יחיד
- משמעות אבטחתית:
- אם 3 היה מחלק את $p-1$ או $q-1$, אז לחלק מההודעות היו מספר פתרונות אפשריים, מה שהיה פוגע בחד-משמעיות הפענוח
- הניתוח שעשינו מדגים מדוע יש להקפיד על בחירה נכונה של הפרמטרים ב-RSA
בפועל, בהצפנת RSA משתמשים במעריכים גדולים יותר מ-3 מסיבות אבטחה, אך העיקרון המתמטי זהה.
Euclidean Algorithm
import math
subscript = {
0: '₀', 1: '₁', 2: '₂', 3: '₃', 4: '₄',
5: '₅', 6: '₆', 7: '₇', 8: '₈', 9: '₉'
}
def extended_gcd(a,b,m=1):
print(f'i | r | q | s | t')
a_prev = a
b_prev = b
q = []
t_prev = 0
t = 1
s_prev = 1
s = 0
i = 1
q = math.floor(a_prev // b_prev * 1.0)
r = a_prev - q* b_prev
print(f'0 | r{subscript[0]}={b:3} | ' + \
f' | s{subscript[0]}={s_prev:3} | t{subscript[0]} = {t_prev:3}')
while r > 0:
temp = t_prev - q * t
t_prev = t
t = temp
temp = s_prev - q * s
s_prev = s
s = temp
a_prev = b_prev
b_prev = r
q = math.floor(a_prev // b_prev * 1.0)
print(f'{i} | r{subscript[i]}={r:3} | q{subscript[i]}={q:3}' + \
f' | s{subscript[i]}={t:3} | t{subscript[i]} = {s:3}')
r = a_prev - q* b_prev
i+=1
r = b_prev
return r, s, t
# extended_gcd(28,75)
# print()
a = 84
b = 154
print(extended_gcd(a,b))
r, s, t = extended_gcd(a,b)
print(f'checking if {s}*{a}+({t})*{b}={r}... {s*a+t*b == r}!')
import math
subscript = {
0: '₀', 1: '₁', 2: '₂', 3: '₃', 4: '₄',
5: '₅', 6: '₆', 7: '₇', 8: '₈', 9: '₉'
}
def gcd(a,b,m=1):
r_m_prev = a
r_m = b
m = 1
q = []
print(f'r₀ = {a}, r₁ = {b}')
while r_m != 0:
q_m = math.floor(r_m_prev // r_m * 1.0)
q.append(q_m)
t = r_m_prev
r_m_prev = r_m
r_m = t - q_m*r_m
print(f'{q_m*r_m_prev+r_m}={q_m}*{r_m_prev} + {r_m} (q{subscript[m]}={q_m}, r{subscript[m+1]}={r_m})')
m +=1
r_m = max(r_m_prev, 1)
return q, r_m
# gcd(98,115)
print(gcd(84, 154))